정화 코딩
EDOC 2024-1 5회차 과제 (동적 계획법 알아보기 3) 본문
090. LCS 2 (백준 9252번)

https://www.acmicpc.net/problem/9252
import sys
input = sys.stdin.readline
str1 = input().strip()
str2 = input().strip()
len1 = len(str1)
len2 = len(str2)
dp = [[0 for _ in range(len2 + 1)] for _ in range(len1 + 1)]
memo = [[0 for _ in range(len2 + 1)] for _ in range(len1 + 1)]
for i in range(1, len1 + 1):
for j in range(1, len2 + 1):
if str1[i - 1] == str2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
memo[i][j] = "↖"
else:
if dp[i - 1][j] >= dp[i][j - 1]:
dp[i][j] = dp[i - 1][j]
memo[i][j] = "↑"
else:
dp[i][j] = dp[i][j - 1]
memo[i][j] = "←"
print(dp[len1][len2]) # LCS의 길이 출력
ans = ""
i = len1
j = len2
while i > 0 and j > 0:
if memo[i][j] == "↖":
ans = ans + str1[i - 1]
i -= 1
j -= 1
elif memo[i][j] == "↑":
i -= 1
else:
j -= 1
# LCS 출력
for i in range(len(ans) - 1, -1, -1):
print(ans[i], end = "")며칠전에 컴퓨터알고리즘 과제로 이미 구혔했던 알고리즘이라서 쉽게 풀었다. (정답)
첫번째 문자열의 i번째 문자까지와 두번째 문자열의 j번째 문자까지의 LCS를 dp[i][j]이라고 하자.
첫번째 문자열의 i번째 문자와 두번째 문자열의 j번째 문자가 같다면, dp[i][j] = dp[i-1][j-1]
첫번째 문자열의 i번째 문자와 두번째 문자열의 j번째 문자가 다르다면, dp[i][j] = max(dp[i-1][j], dp[i][j-1])
(dp를 채워나가면서 나중에 LCS를 출력하기 위해 배열 memo에 기록해둔다.)
091. 가장 큰 정사각형 (백준 1915번)

https://www.acmicpc.net/problem/1915
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
dp = []
maxS = 0
for i in range(n):
dp.append(list(map(int, list(input().strip()))))
for j in range(m):
if dp[i][j] == 1 and i > 0 and j > 0:
dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
if maxS < dp[i][j]:
maxS = dp[i][j]
print(maxS * maxS)아이디어가 잘 안 떠올라서 교재를 참고하여 풀었다. (정답) 점화식 자체는 간단한데 점화식이 도출되는 과정이 교재 설명만으로는 잘 이해가 안 되는 것 같아 구글링을 통해 이해해보고 정리해봤다.
dp[i][j]: (i, j)의 칸을 포함하는 정사각형 중 가장 큰 정사각형의 크기
→ dp 배열의 의미를 이렇게 정한 이유? 이렇게 잡아야 다음 칸과의 연관성이 생기고 점화식을 세울 수 있기 때문

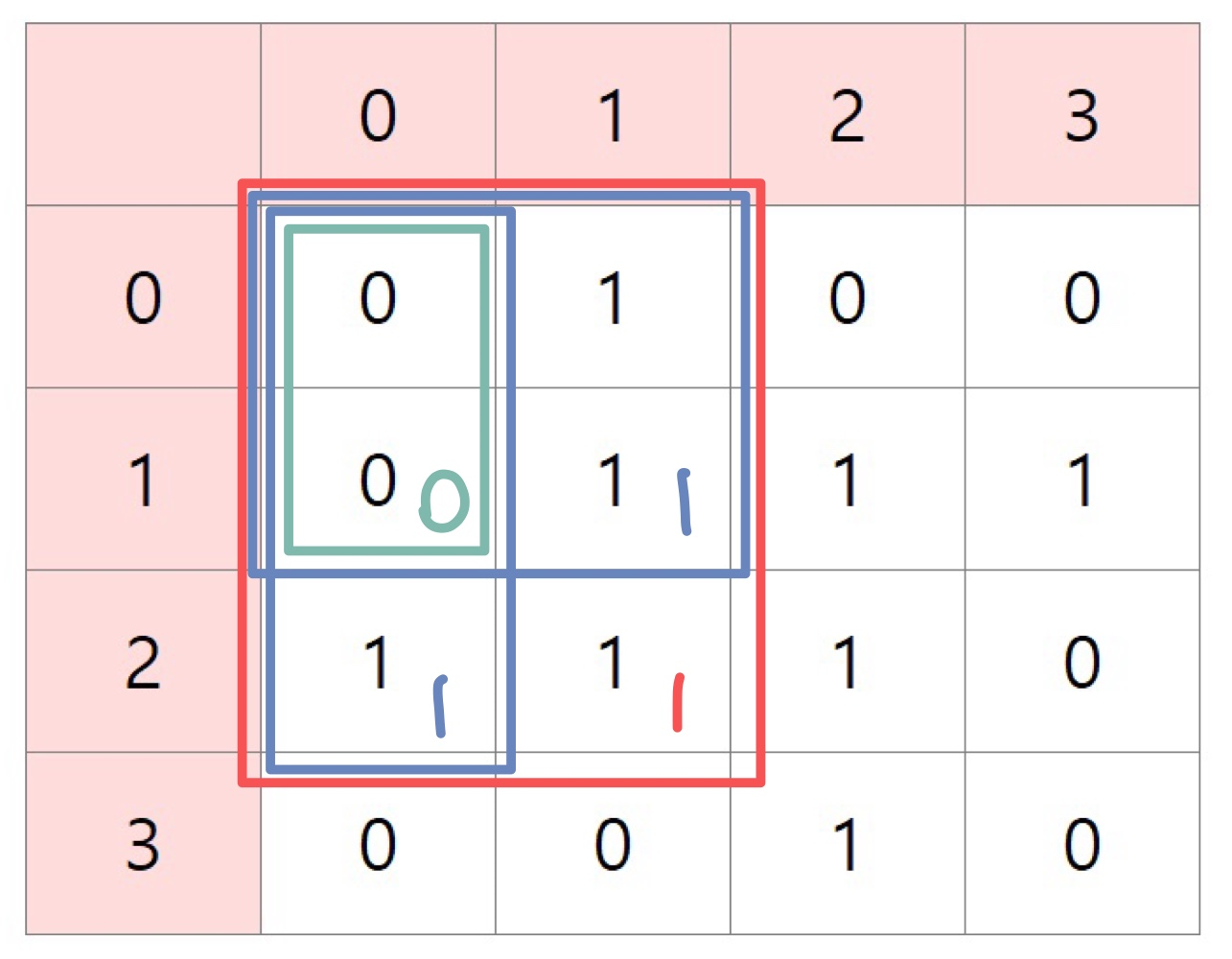


즉, 위쪽, 왼쪽, 대각선 3개의 값 중 가장 작은 값에 의하여 잘리게 되므로 그 중 가장 작은 값 + 1 (해당 칸의 1)이 되는 것이다. 당연히 이 점화식은 해당 칸이 1일 때만 수행된다.
⇒ dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
092. 고층 건물 (백준 1328번)

https://www.acmicpc.net/problem/1328
import sys
input = sys.stdin.readline
mod = 1000000007
n, l, r = map(int, input().split())
dp = [[[0 for _ in range(n + 1)] for _ in range(n + 1)] for _ in range(n + 1)]
dp[1][1][1] = 1
for i in range(2, n + 1):
for j in range(1, l + 1):
for k in range(1, r + 1):
dp[i][j][k] = (dp[i - 1][j][k] * (i - 2) + dp[i - 1][j][k - 1] + dp[i - 1][j - 1][k]) % mod
print(dp[n][l][r])너무 어려워서 거의 교재를 보고 풀었다. (정답)
빌딩 수를 하나씩 늘려가면서 값을 구해나가야 하는데, 이 때 매 순간마다 추가되는 빌딩이 가장 낮은 빌딩이라면 왼쪽에서 볼 때의 빌딩 수와 오른 쪽에서 볼 때의 빌딩 수가 확정적으로 정해진다. 즉, 빌딩을 높은 것부터 낮은 것 순으로 추가하면 상황이 단순화되기 때문에 점화식을 세우는 것이 가능해지는 것이다.
dp[n][l][r], 즉 n개의 빌딩이 있고 왼쪽에서 l개 오른쪽에서 r개가 보일 수 있는 경우의 수를 구해보자.
왼쪽에 빌딩을 추가하면 왼쪽 빌딩 1개 증가함 → dp[n-1][l-1][r]
오른쪽에 빌딩을 추가하면 오른쪽 빌딩 1개 증가함 → dp[n-1][l][r-1]
가운데에 빌딩을 추가하면 변화 없음 → dp[n-1][l][r] * (n-2)
⇒ dp[i][j][k] = dp[i - 1][j][k] * (i - 2) + dp[i - 1][j][k - 1] + dp[i - 1][j - 1][k]
'Group > EDOC' 카테고리의 다른 글
| EDOC 2024-1 7회차 정모 준비 (이분 탐색, 다이나믹) (0) | 2024.05.22 |
|---|---|
| EDOC 2024-1 6회차 과제 (동적 계획법 알아보기 4) (1) | 2024.05.18 |
| EDOC 2024-1 5회차 정모 (동적 계획법 알아보기 2) (0) | 2024.05.12 |
| EDOC 2024-1 5회차 정모 준비 (정렬, 다이나믹) (1) | 2024.05.08 |
| EDOC 2024-1 4회차 과제 (동적 계획법 알아보기 2) (1) | 2024.05.04 |




