정화 코딩
EDOC 2024-1 5회차 정모 준비 (정렬, 다이나믹) 본문
거리의 합 2 (백준 23330번)

https://www.acmicpc.net/problem/23330
문제 해석
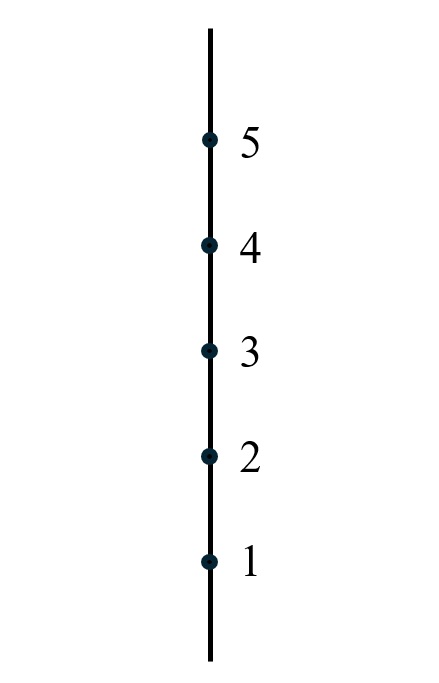
이런식으로 n개의 점이 수직선 위에 놓여 있고, 모든 점들의 쌍에 대해 두 점 사이의 거리의 합을 구하는 문제이다.
첫번째 풀이
우선 가장 직관적인 풀이로 풀어보자.
//C++
#include <iostream>
#include <vector>
#include <cstdlib>
using namespace std;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
vector<int> data(n);
for (int i = 0; i < n; i++) {
cin >> data[i];
}
long long sum = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
sum += abs(data[i] - data[j]);
}
}
cout << sum << '\n';
}모든 점의 조합에 대해 두 점 사이의 거리를 더하면 되므로 이중 for문으로 간단히 풀 수 있다. 하지만 이렇게 풀게 되면 시간 복잡도는 O(n^2)이므로 시간 초과가 발생한다.

cf. 절댓값 함수 abs()를 쓰기 위해 #include <cstdlib>를 넣어주었다.
두번째 풀이
풀이를 최적화시키기 위해 좀 더 생각해보자.
각 수 별로 해당 수가 사용된 연산들을 정리해보면 다음과 같다.
5 -> abs(5-5) abs(5-4) abs(5-3) abs(5-2) abs(5-1)
abs(4-5)
abs(3-5)
abs(2-5)
abs(1-5)
4 -> abs(5-4)
abs(4-5) abs(4-4) abs(4-3) abs(4-2) abs(4-1)
abs(3-4)
abs(2-4)
abs(1-4)
3 -> abs(5-3)
abs(4-3)
abs(3-5) abs(3-4) abs(3-3) abs(3-2) abs(3-1)
abs(2-3)
abs(1-3)
2 -> abs(5-2)
abs(4-2)
abs(3-2)
abs(2-5) abs(2-4) abs(2-3) abs(2-2) abs(2-1)
abs(1-2)
1 -> abs(5-1)
abs(4-1)
abs(3-1)
abs(2-1)
abs(1-5) abs(1-4) abs(1-3) abs(1-2) abs(1-1)각 수가 들어가는 연산들 중, 그 수가 더하기로 쓰이는 연산이 몇 개이고 빼기로 쓰이는 연산이 몇 개인지 세어보자.
예를 들어, 5가 들어가는 연산들 중, 5가 더하기로 쓰이는 연산은 9개이고 빼기로 쓰이는 연산은 1개이다.
5 ⇒ (+9) + (-1) = +8
4 ⇒ (+7) + (-3) = +4
3 ⇒ (+5) + (-5) = 0
2 ⇒ (+3) + (-7) = -4
1 ⇒ (+1) + (-9) = -8
이제 일반화해보자.
i번째 수(i는 인덱스)에 대해, 더하기에 쓰이는 연산은 (2i + 1)개이고 빼기로 쓰이는 연산은 (2n - (2i + 1))개이다.
오름차순 정렬된 상태에서 data[i]와 관련된 연산의 합은 (4i -2n +2) * data[i]이다.
이를 활용하여 다시 코드를 짜면 다음과 같다.
//C++
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
vector<long long> data(n);
for (int i = 0; i < n; i++) {
cin >> data[i];
}
sort(data.begin(), data.end());
long long sum = 0;
for (int i = 0; i < n; i++) {
sum += (4 * i - 2 * n + 2) * data[i];
}
cout << sum << '\n';
}정렬함수 sort()를 사용하기 위해 #include <algorithm>를 넣어주었다.
sort()의 시간 복잡도 O(nlogn) : algorithm 헤더파일에서 제공하는 sort()는 intro sort라는 algorithm으로 구현되어 있다. intro sort는 세 가지 정렬법(quick sort, heap sort, insertion sort)을 섞은 방식이다. intro sort는 최악의 경우에 O(n^2)의 시간 복잡도를 갖는 quick sort의 단점을 보완하여, 어떤 경우에라도 O(nlogn)의 시간 복잡도를 보장해주는 정렬법이다.
sort()로 vector 정렬하는 법 : sort(v.begin(), v.end());
주의할 점: 첫번째 풀이와 달리 sum에 더해지는 값이 int 범위를 넘어갈 수 있기 때문에 자료형에 주의해야 한다. 이 풀이에서는 data의 자료형을 long long으로 바꿔주었다.
이 풀이의 시간 복잡도는 O(nlogn)이다. (정렬하는 부분을 빼면 O(n), 정렬 때문에 O(nlogn)이 됨.)
평범한 배낭 (백준 12865번)

https://www.acmicpc.net/problem/12865
문제 해석
이 문제는 담을 수 있는 최대 무게가 정해져 있는 가방에 최대한 가치가 높도록 물건을 골라담는 문제이다. 이러한 류의 문데를 배낭 문제라고 한다. 배낭 문제는 두 가지 종류로 나눌 수 있다.
1) Fraction Knapsack Problem : 물건을 쪼갤 수 있는 배낭 문제 → 그리디 알고리즘
2) 0/1 Knapsack Problem : 물건을 쪼갤 수 없는 배낭 문제 → 다이나믹 프로그래밍
이 문제는 물건을 쪼갤 수 없는 0/1 Knapsack Problem에 해당하므로 다이나믹 프로그래밍을 통해 해결해야 한다.
풀이
문제의 입력을 표로 정리하면 다음과 같다.
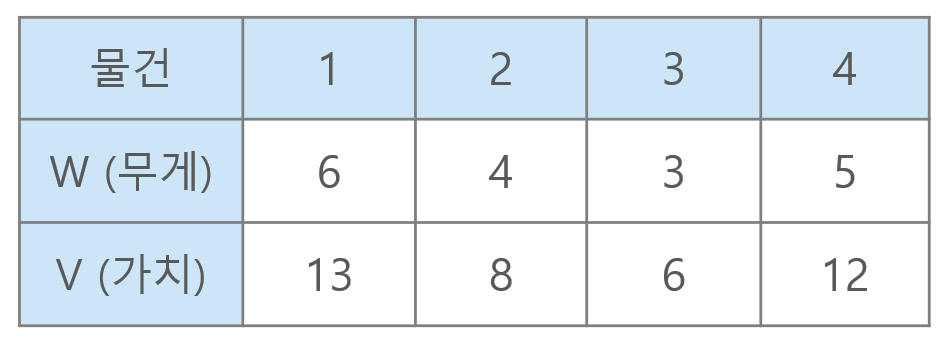
이제 dp 테이블을 채워보자. 가방 무게가 1일 때, 2일 때, 3일 때, ... 이런식으로 가방 무게를 1씩 늘려간다. 그리고 가방 무게가 1일 때, 물건1까지 살펴보고, 그 다음에는 물건2까지 살펴보고, ... 이런식으로 물건을 하나하나 살펴볼 것이다.
dp[i][j] : 가방의 무게가 i이고, j번째 물건까지 살펴봤을 때, 가방에 담을 수 있는 최대 가치
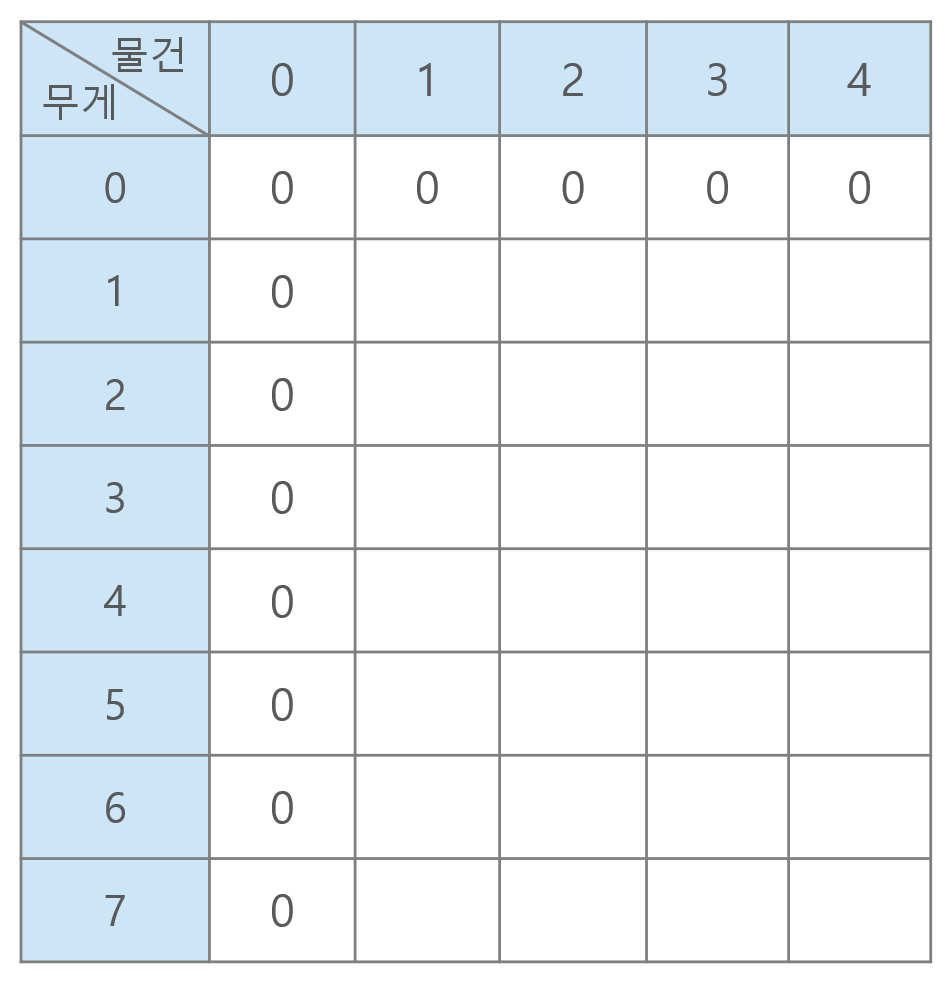


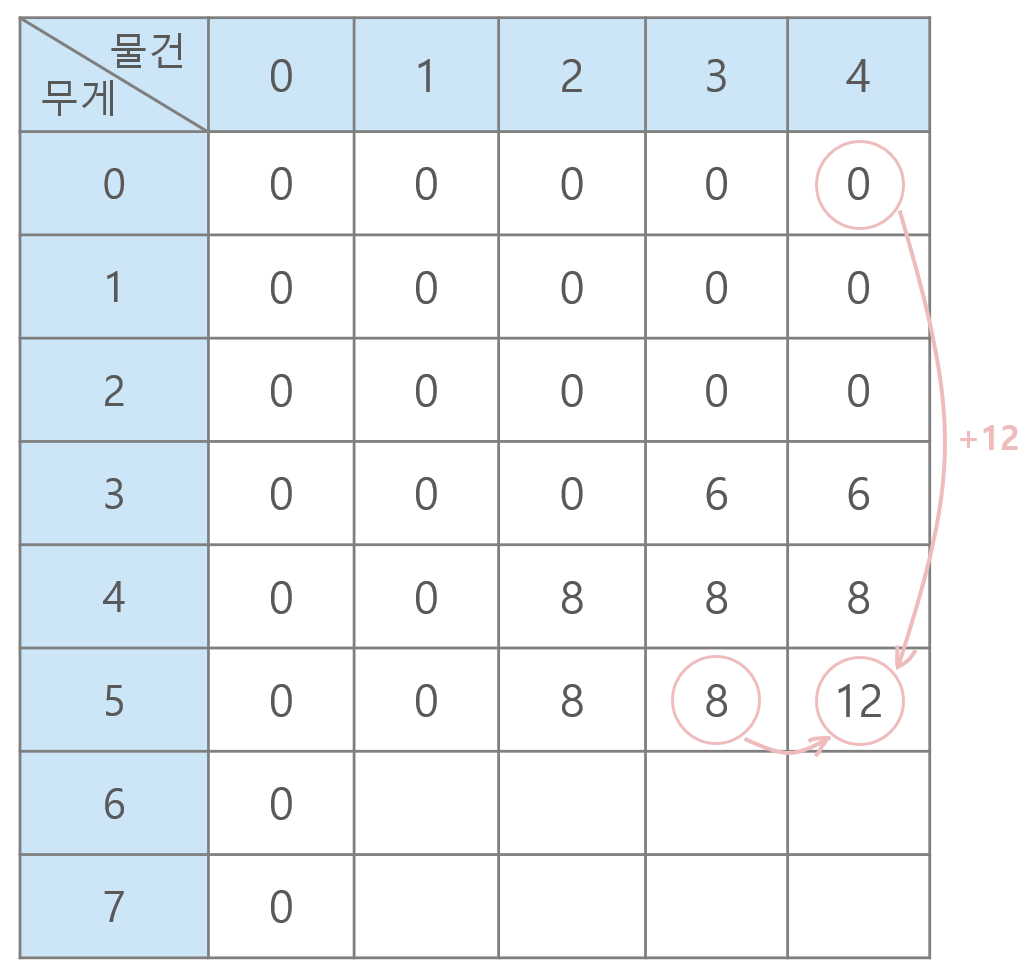
이 때, 12라는 수가 나오는 과정은 다음과 같다. 물건4를 넣는 것이 최적이 아닐 경우에는 물건3까지 본 결과와 같을 것이고, 물건4를 넣는 것이 최적일 경우에는 일단 물건4의 무게만큼 가방에서 빼고 그 상태에서 물건4를 넣은 결과가 될 것이다.
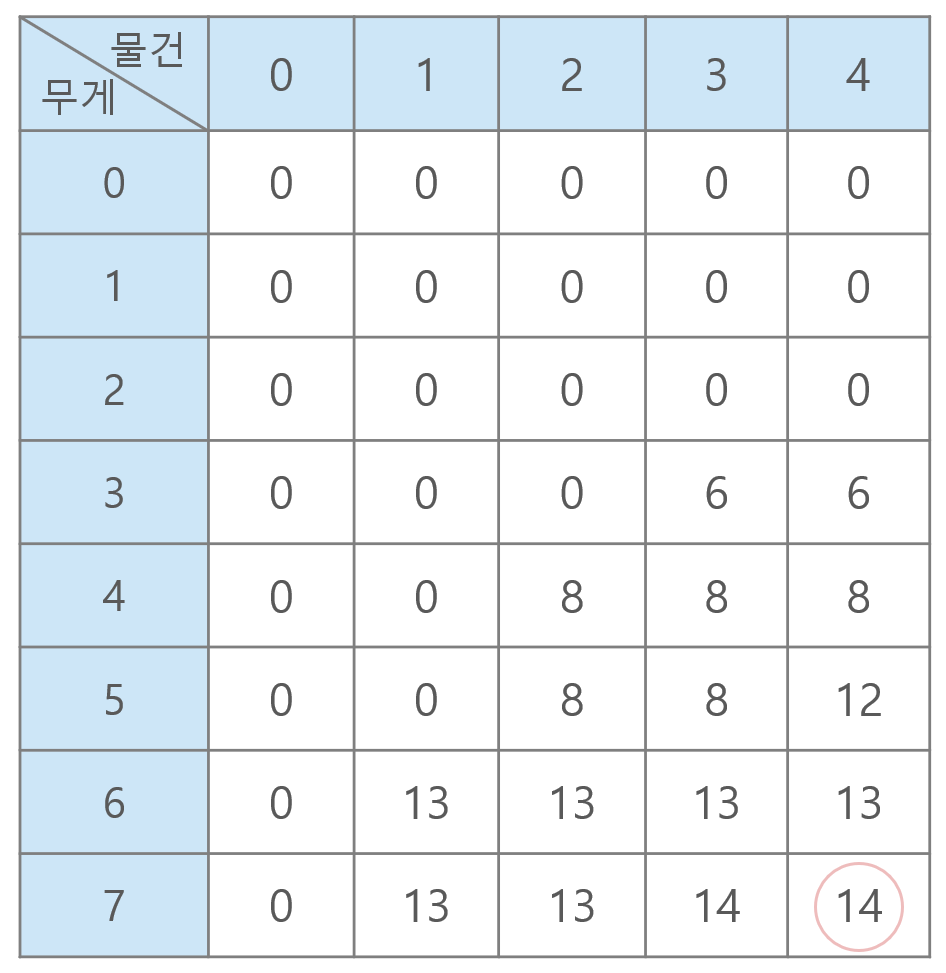
즉, 해당 물건의 무게가 가방 무게보다 작은 경우에는, 그 물건을 넣지 않는 것이 나은지 넣는 것이 나은지 확인해서 더 가치가 높은 값을 취한다. 해당 물건의 무게가 가방 무게보다 큰 경우에는, 그 물건을 넣을 수 없으므로 확인할 필요없이 그 전 물건까지 확인한 결과를 그대로 가져온다.
이를 점화식으로 적으면 다음과 같다.
if w[j] <= i:
dp[i][j] = max(dp[i][j - 1], dp[i - w[j]][j - 1] + v[j])
else:
dp[i][j] = dp[i][j - 1]이제 이를 토대로 전체 코드를 작성해보자.
#python
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
dp = [[0 for _ in range(n + 1)] for _ in range(k + 1)]
w = [0] * (n + 1)
v = [0] * (n + 1)
for i in range(1, n + 1):
w[i], v[i] = map(int, input().split())
for i in range(1, k + 1):
for j in range(1, n + 1):
if w[j] <= i:
dp[i][j] = max(dp[i][j - 1], dp[i - w[j]][j - 1] + v[j])
else:
dp[i][j] = dp[i][j - 1]
print(dp[k][n])
'Group > EDOC' 카테고리의 다른 글
| EDOC 2024-1 5회차 과제 (동적 계획법 알아보기 3) (0) | 2024.05.12 |
|---|---|
| EDOC 2024-1 5회차 정모 (동적 계획법 알아보기 2) (0) | 2024.05.12 |
| EDOC 2024-1 4회차 과제 (동적 계획법 알아보기 2) (1) | 2024.05.04 |
| EDOC 2024-1 4회차 정모 (동적 계획법 알아보기 1) (0) | 2024.04.10 |
| EDOC 2024-1 3회차 과제 (동적 계획법 알아보기 1) (0) | 2024.04.07 |




