정화 코딩
EDOC 2024-1 7회차 정모 준비 (이분 탐색, 다이나믹) 본문
공유기 설치 (백준 2110번)

https://www.acmicpc.net/problem/2110
문제 해석

문제에서 주어진 예제를 그려보면 이렇게 된다. 1, 2, 4, 8, 9 위치에 집이 배치되어 있다. 이런 상황에서 가장 인접한 두 공유기 사이의 최대 거리는 공유기를 1, 4, 8에 설치하는 경우와 1, 4, 9에 설치하는 경우 모두 3이 된다.
이런 답은 어떤 과정으로 나오는 것일까? 우선 이 문제를 코드로 해결하는 게 아닌 인간인 우리가 푼다고 생각해보자. '대충 간격을 4 이상으로 둬볼까? 아 4이상으로 하니까 공유기가 남네... 그러면 좀 더촘촘히 둬도 될 것 같으니까 간격을 더 늘려서.....' 이런식으로 푸는 것이 자연스러워 보인다. 이런 경우에 사용되는 알고리즘이 이분 탐색이다.
풀이
//C++
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, c;
cin >> n >> c;
vector<int> home = vector<int>(n);
for (int i = 0; i < n; i++) {
cin >> home[i];
}
sort(home.begin(), home.end());
int l = 1;
int r = home[n - 1] - home[0] + 1;
int m;
while (l < r) {
m = (l + r) / 2;
int cnt = 1;
int pre = home[0];
for (int x: home) {
if ((x - pre) >= m) {
cnt++;
pre = x;
}
}
if (cnt >= c) {
l = m + 1;
}
else {
r = m;
}
}
cout << (l - 1) << '\n';
}home: 각 집의 위치 (좌표)
가장 먼저 해야할 것은 home을 정렬하는 것이다. 좌표 상 왼쪽인 집이 왼쪽으로 오도록 오름차순 정렬을 해준다.
l : inclusive / r : exclusive ⇒ while 반복문 조건 : l < r
공유기 사이 간격의 최솟값은 집과 집 사이의 최소 거리인 1이다. ⇒ int l = 1;
공유기 사이 간격의 최댓값은 첫번째 집과 마지막 집 사이의 거리이다. ⇒ int r = home[n - 1] - home[0] + 1;
cnt : 공유기를 m 간격으로 둔다고 할 때 필요한 공유기의 개수
cnt >= c 이면 l = m + 1 로 바꿔주고 다시 탐색
cnt < c 이면 r = m 으로 바꿔주고 다시 탐색
while문이 끝나고 l에 담겨 있는 값의 의미 : 간격을 점점 늘려갈 때, 처음으로 공유기가 남는 순간의 간격
따라서 우리가 구하고자 하는 답은 (l - 1)이다. (공유기를 딱 c개 쓰면서 가장 큰 간격)
이 코드를 문제에서 주어진 예제에 적용해보면 다음과 같다.
home = [1, 2, 4, 8, 9]
l = 1 // 초기값
r = 10 // 초기값
m = (1 + 10) / 2 = 5 -> cnt = 2 -> r = 5
m = (1 + 5) / 2 = 3 -> cnt = 3 -> l = 4
m = (4 + 5) / 2 = 4 -> cnt = 2 -> r = 4
ans = l - 1 = 3
전깃줄 (백준 2565번)


https://www.acmicpc.net/problem/2565
문제 해석
두 전깃줄이 교차한다는 것이 무슨 의미일까? 전깃줄 1과 전깃줄 2에 대해, 전봇대 A쪽에서는 전깃줄 1이 더 위에 있고 전봇대 B쪽에서는 전깃줄 2가 더 위에 있다는 의미이다. 전깃줄이 어떤식으로 교차되어 있는지를 쉽게 보기 위해서는 한 전봇대를 기준으로 정렬하는 것이 좋다.
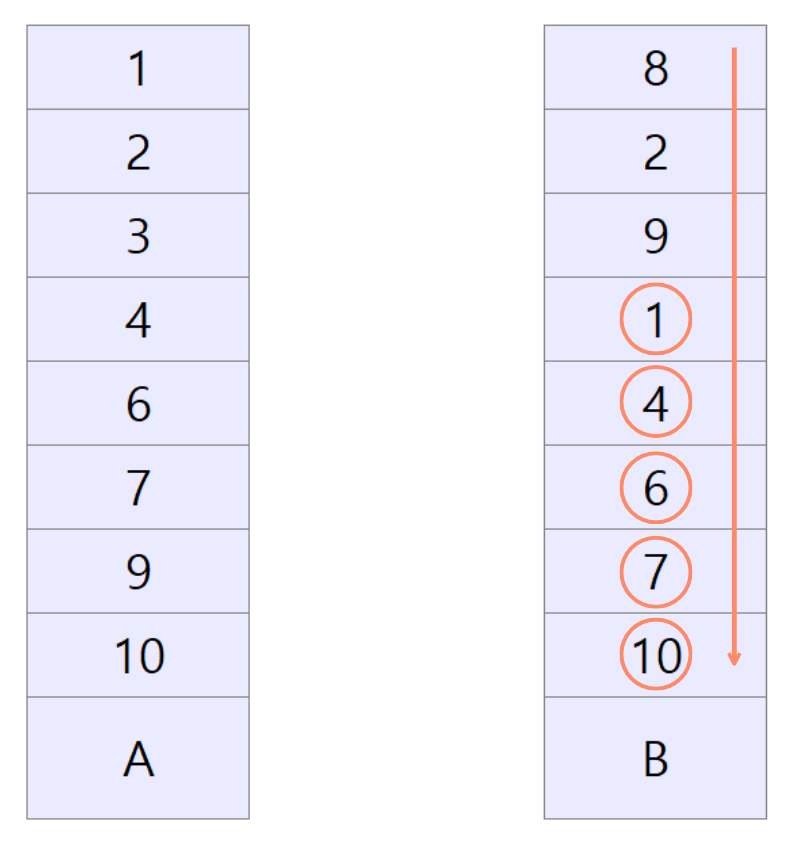
A에서 증가함에 따라 B에서도 증가하기만 하면 전깃줄은 하나도 교차하지 않는 것이다. 하지만 B에서 증가 수열을 방해하는 원소들이 전깃줄이 교차하도록 만드는 전깃줄이라고 생각할 수 있다. 우리의 목표는 전깃줄이 하나도 겹치지 않게 하는 것이기 때문에 증가 수열을 방해하는 원소들을 제거해주면 된다. 여기까지 이해하면 가장 긴 증가하는 부분 수열을 구한 문제랑 동일하다는 것을 알 수 있다.
풀이
//C++
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
vector<vector<int>> line = vector<vector<int>>(n + 1, vector<int>(2));
line[0][0] = line[0][1] = 0;
for (int i = 0; i < n; i++) {
cin >> line[i][0] >> line[i][1];
}
sort(line.begin(), line.end());
int maxa = 0;
vector<int> dp = vector<int>(n + 1, 0);
dp[0] = 0;
for (int i = 1; i < n + 1; i++) {
int maxt = 0;
for (int j = 0; j < i; j++) {
if (line[i][1] >= line[j][1]) {
maxt = max(maxt, dp[j] + 1);
}
}
dp[i] = maxt;
maxa = max(maxa, dp[i]);
}
cout << (n - maxa) << '\n';
}
앞의 계산을 뒤의 계산에서 활용하기 위해서 마지막 요소를 포함시켜 점화식을 정의해야 한다.
dp[i] : 0부터 i까지 i를 포함하는 가장 길게 증가하는 수열의 길이
점화식 : dp[i] = max(dp[k]) + 1 (dp[i]보다 dp[k]가 작은 0과 i-1 사이의 k에 대해...)
'Group > EDOC' 카테고리의 다른 글
| EDOC 2024-1 7회차 과제 (기하 알아보기) (0) | 2024.05.26 |
|---|---|
| EDOC 2024-1 7회차 정모 (동적 계획법 알아보기 4) (1) | 2024.05.25 |
| EDOC 2024-1 6회차 과제 (동적 계획법 알아보기 4) (1) | 2024.05.18 |
| EDOC 2024-1 5회차 과제 (동적 계획법 알아보기 3) (0) | 2024.05.12 |
| EDOC 2024-1 5회차 정모 (동적 계획법 알아보기 2) (0) | 2024.05.12 |




