정화 코딩
EDOC 2024-1 2회차 과제 (조합 알아보기 2) 본문
080. 조약돌 꺼내기 (백준 13251번)

https://www.acmicpc.net/problem/13251
import sys
input = sys.stdin.readline
m = int(input()) # 조약돌 색 종류
color = list(map(int, input().split())) # 색 별 조약돌의 수
k = int(input()) # 뽑는 조약돌의 수
n = sum(color) # 전체 조약돌 수
ans = 0
for x in color:
if x >= k:
tmp = 1
for i in range(k):
tmp *= ((x - i) / (n - i))
ans += tmp
print(ans)오잉 다이나믹도 아니고 조합 구할 필요도 없는 문제였잖아..???? 문제 풀기 전에 생각을 하자... (정답)
081. 순열의 순서 (백준 1722번)

https://www.acmicpc.net/problem/1722
import sys
input = sys.stdin.readline
n = int(input())
data = list(map(int, input().split()))
f = [0 for _ in range(n)]
used = [0 for _ in range(n + 1)]
f[n - 1] = 1
for i in range(1, n):
f[n - i - 1] = f[n - i] * (i + 1)
if data[0] == 1:
k = data[1]
ans = [0 for _ in range(n)]
for i in range(n - 1):
idx = 1
while k > f[i + 1]:
idx += 1
k -= f[i + 1]
for j in range(1, n + 1):
if used[j] == 0:
idx -= 1
if idx == 0:
ans[i] = j
used[j] = 1
break
for j in range(1, n + 1):
if used[j] == 0:
ans[n - 1] = j
for x in ans:
print(x, end=' ')
elif data[0] == 2:
ans = 1
for i in range(1, n):
cnt = 0
for j in range(1, n + 1):
if used[j] == 0:
cnt += 1
if data[i] == j:
used[j] = 1
break
ans += (cnt - 1) * f[i]
print(ans)특정 숫자에 대해서 푸는 건 할 수 있겠는데 (당연함.. 그걸 누가 못 풀어) 일반적인 경우에는 어떻게 풀어야 할지 감이 잘 안 와서 책에서 팩토리얼에 대한 배열을 만들어둔다는 부분을 보고 힌트를 얻었다. 팩토리얼을 배열로 만든다는 것은 그만큼 팩토리얼이 많이 쓰인다는 것!
팩토리얼을 어떻게 쓸까?
0개의 수의 자리가 정해진 경우 → 5개 수의 자리를 정하는 경우 → 5! (f[0])
1개의 수의 자리가 정해진 경우 → 4개 수의 자리를 정하는 경우 → 4! (f[1])
2개의 수의 자리가 정해진 경우 → 3개 수의 자리를 정하는 경우 → 3! (f[2])
... 이런식으로 팩토리얼을 활용할 수 있었다. 팩토리얼 배열: f
소문제 번호가 1일 때
k가 f[1]보다 크면 그 자리에 남은 수 중 가장 작은 수가 들어오면 안 된다는 뜻! → k가 f[1]보다 작거나 같아질 때까지 f[1]씩 빼보면서 어느 수가 들어가야 하는지 체크
k가 f[1]보다 작거나 같으면 그 자리에는 남은 수 중 가장 작은 수가 들어가야 된다는 것 확정!
그 후에는 들어가야 하는 수를 ans 배열에 추가해주고, used 배열을 통해 사용했다는 것 표시.
... 반복
소문제 번호가 2일 때
입력 list를 앞에서부터 보면서 아직 사용하지 않은 수들 중 자신보다 작은 수를 카운트해서 그 개수(cnt - 1)를 저장. ans에 (cnt - 1) * f[1] 더하기!
... 반복
(정답)
082. 사전 (백준 1256번)

https://www.acmicpc.net/problem/1256
import sys
input = sys.stdin.readline
n, m, k = map(int, input().split())
dp = [[0 for _ in range(n + m + 1)] for _ in range(n + m + 1)]
ans = ''
dp[0][0] = 1
for i in range(1, n + m + 1):
dp[i][0] = dp[i][i] = 1
for j in range(1, i):
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
if k > dp[n + m][n]:
print(-1)
else:
while n > 0 or m > 0:
tmp = dp[n + m - 1][n - 1]
if k < tmp: # 그 자리에 a 확정
n -= 1
ans += 'a'
elif k > tmp: # 그 자리에 z 확정
k -= tmp
m -= 1
ans += 'z'
else: # k < tmp -> 그 자리에 a 확정 & 나머지 문자들도 확정
n -= 1
ans += ('a' + 'z' * m + 'a' * n)
break
print(ans)
n개의 'a'와 m개의 'z'가 있는 상황.
앞에서부터 각 자리에 들어갈 알파벳을 정해줄 것임. 현재 자리에 일단 a를 넣고 a를 썼다고 가정한 상태에서 생각한다. 나머지 자리들의 알파벳들을 결정할 경우의 수는 (n+m-1)C(n-1)이다. 여기서 (n+m-1)는 a 하나를 이미 썼다고 가정한 상태에서 전체 개수이고 (n-1) a 하나를 이미 썼다고 가정한 상태에서 a의 개수이다.
k < (n+m-1)C(n-1) → 그 자리가 a 자리가 맞다는 것! 실제로 a의 개수를 하나 줄여주고 ans에 a를 추가해줌.
k > (n+m-1)C(n-1) → 그 자리가 a 자리가 아니라 z 자리라는 것! k값 다시 조정해주고, z의 개수를 하나 줄여주고 ans에 z를 추가해줌.
k == (n+m-1)C(n-1) → 그 자리에 a 확정! + 나머지 자리들도 같이 확정됨. (a는 다 앞으로 z는 다 뒤로) ans에 그에 맞게 추가해주고 break.
(정답)
083. 선물 전달 (백준 1947번)
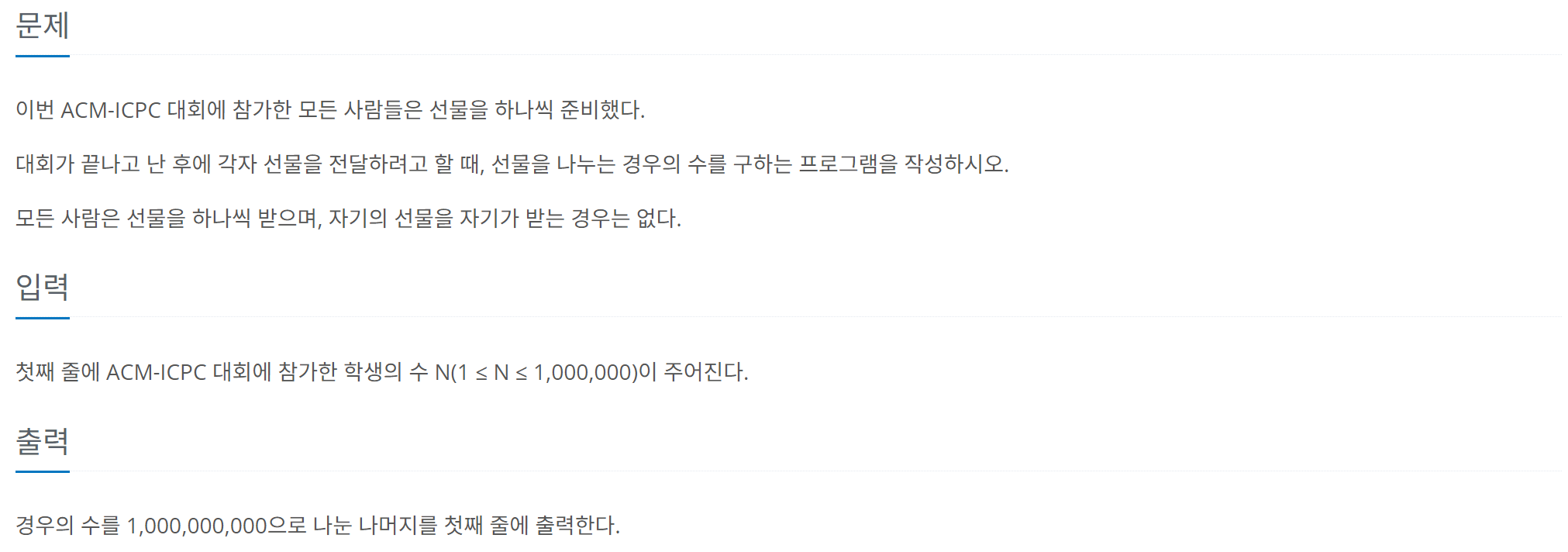
https://www.acmicpc.net/problem/1947
import sys
input = sys.stdin.readline
mod = 1000000000
n = int(input())
dp = [0 for _ in range(1000001)]
dp[2] = 1
for i in range(3, n + 1):
dp[i] = (i - 1) * (dp[i - 2] + dp[i - 1])
dp[i] %= mod
print(dp[n])
일단 잘 모르겠으니 적어보면서 규칙을 찾아보려고 했다. 그런데 풀다보니 고등학교 확률과 통계에서 주구장창 풀었던 것 같은 익숙함... 검색해보니 완전 순열(교란 순열)이라고 한다. 고등학생 때는 교란 순열 점화식을 그냥 외우거나 몇 개 적어보면서 규칙을 생각해내거나 했던 것 같은데, 그 원리는 이번에 처음 알게 되었다.
완전 순열(교란 순열)?
모든 원소의 위치를 바꾸는 순열
규칙과 점화식
dp[1] = 0, dp[2] = 1, dp[3] = 2, dp[4] = 9, dp[5] = 44, ...
⇒ dp[n] = (n - 1) * (dp[n - 2] + dp[n - 1]) (n >= 3)
원리
1이 선물을 k에게 주었다.
1) k도 1에게 준 경우: 나머지 n-2에 대해 완전 순열. ⇒ dp[n - 2]
2) k는 1이 아닌 다른 사람에게 준 경우: 1과 k를 같은 것으로 취급. 1(=k)을 제외한 n-1에 대해 완전 순열. ⇒ dp[n - 1]
여기서 k로 가능한 수는 1을 제외한 전부이므로 n-1 ⇒ 1)과 2)를 합친 것에 (n - 1)을 곱해줌.
(정답)
'Group > EDOC' 카테고리의 다른 글
| EDOC 2024-1 3회차 과제 (동적 계획법 알아보기 1) (0) | 2024.04.07 |
|---|---|
| EDOC 2024-1 3회차 정모 (조합 알아보기 2) (1) | 2024.04.07 |
| EDOC 2024-1 2회차 정모 (조합 알아보기 1) (0) | 2024.04.01 |
| EDOC 2024-1 1회차 과제 (조합 알아보기 1) (1) | 2024.03.26 |
| EDOC 2024-1 1회차 정모 (0) | 2024.03.26 |





