정화 코딩
EDOC 2024-1 1회차 과제 (조합 알아보기 1) 본문
10-1. 조합 알아보기
076. 이항 계수 1 (백준 11050번)

https://www.acmicpc.net/problem/11050
from sys import stdin
n, k = map(int, stdin.readline().split())
dp = [[0 for _ in range(n + 1)] for _ in range(n + 1)]
dp[0][0] = 1
for i in range(1, n + 1):
dp[i][0] = dp[i][i] = 1
for j in range(1, i):
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
print(dp[n][k])예전에 팩토리얼로 풀었던 문제. 이렇게 점화식을 이용해서 전체 테이블을 다 채워서 푸는 풀이로는 처음 풀어봤다. 이 문제는 테스트 케이스가 1개로 고정이어서 전자의 방식이 효율적이겠지만, 테스트 케이스가 많아지면 많아질수록 후자의 방식이 효율적일 것이다. 왜냐하면 테이블은 처음에 한번만 계산하면 되고, 그 이후에는 입력이 들어올 때마다 이차원 배열에서 값을 읽어서 출력만 하면 되기 때문이다. (정답)
추가로, 교재와는 살짝 다르게 코드를 짜서 반복문을 2개에서 1개로 줄였다.
077. 이항 계수 2 (백준 11051번)
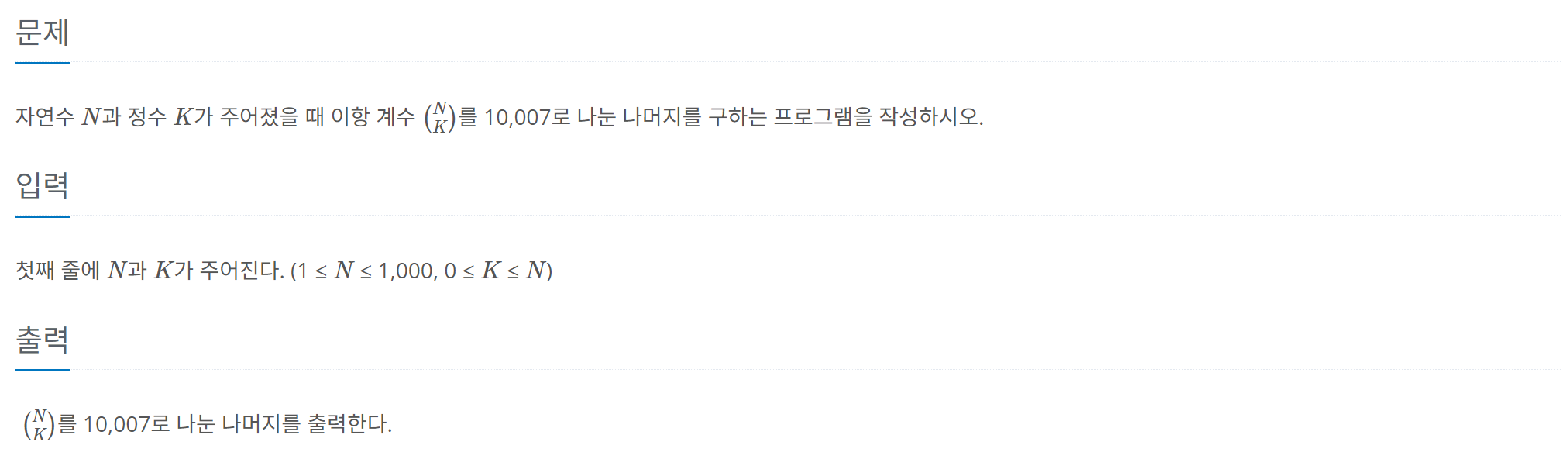
https://www.acmicpc.net/problem/11051
from sys import stdin
mod = 10007
n, k = map(int, stdin.readline().split())
dp = [[0 for _ in range(n + 1)] for _ in range(n + 1)]
dp[0][0] = 1
for i in range(1, n + 1):
dp[i][0] = 1
dp[i][i] = 1
for j in range(1, i):
dp[i][j] = ((dp[i - 1][j - 1] % mod) + (dp[i - 1][j] % mod)) % mod
print(dp[n][k])76번 문제의 풀이에서 10007로 나눠주는 부분만 추가하면 된다. (A mod N + B mod N) mod N = (A + B) mod N을 활용하면 된다. (정답)
078. 부녀회장이 될테야 (백준 2775번)

https://www.acmicpc.net/problem/2775
from sys import stdin
dp = [[0 for _ in range(15)] for _ in range(15)]
for i in range(1, 15):
dp[0][i] = i
for i in range(1, 15):
dp[i][1] = dp[i - 1][1]
for j in range(2, 15):
dp[i][j] = dp[i][j - 1] + dp[i - 1][j]
t = int(stdin.readline())
for _ in range(t):
k = int(stdin.readline())
n = int(stdin.readline())
print(dp[k][n])이것도 풀었던 적 있는 문제. 그런데 이전에 풀었던 풀이에서는 append를 써서 그런걸까..?? 이번 풀이보다 꽤 시간이 걸리는 것으로 보인다. 아무튼 앞에서 조합식을 구할 때 점화식을 구해서 테이블을 만들었던 것처럼, 점화식을 먼저 구하고 그에 맞게 테이블을 채우면 되는 문제였다. (정답)
079. 다리 놓기 (백준 1010번)

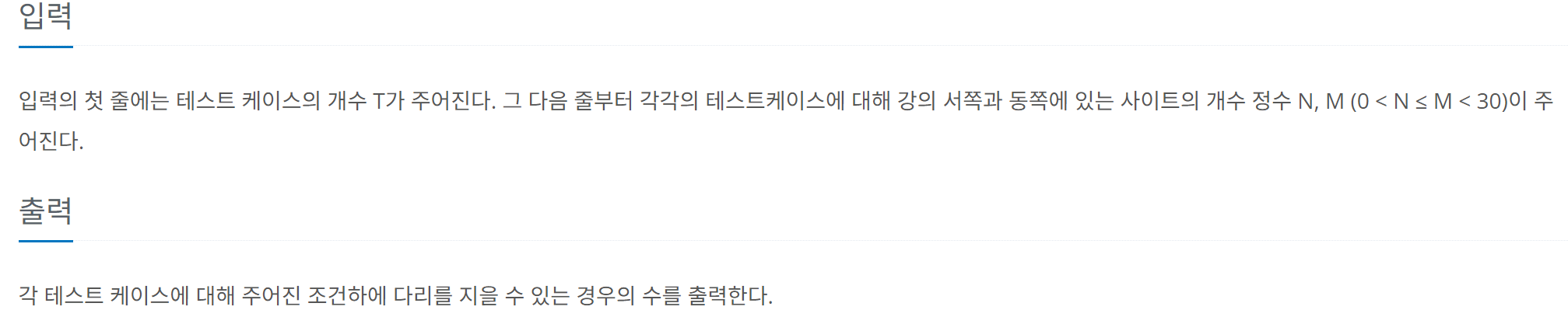
https://www.acmicpc.net/problem/1010
from sys import stdin
dp = [[0 for _ in range(30)] for _ in range(30)]
dp[0][0] = 1
for i in range(1, 30):
dp[i][0] = dp[i][i] = 1
for j in range(1, i):
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
t = int(stdin.readline())
for _ in range(t):
n, m = map(int, stdin.readline().split())
print(dp[m][n])조합을 쓰면 된다는 것만 알면 되는 문제! (정답)
'Group > EDOC' 카테고리의 다른 글
| EDOC 2024-1 2회차 과제 (조합 알아보기 2) (0) | 2024.04.01 |
|---|---|
| EDOC 2024-1 2회차 정모 (조합 알아보기 1) (0) | 2024.04.01 |
| EDOC 2024-1 1회차 정모 (1) | 2024.03.26 |
| EDOC 2023-W 7회차 과제 (최소 공통 조상) (0) | 2024.02.25 |
| EDOC 2023-W 7회차 정모 (이진 트리 / 세그먼트 트리) (0) | 2024.02.20 |




