정화 코딩
EDOC 2023-2 8주차 과제 본문
07-1. 소수 구하기
037. 소수 구하기 (백준 1929번)

https://www.acmicpc.net/problem/1929
from sys import stdin
import math
m, n = map(int, stdin.readline().split())
num = [0] * (n+1)
for i in range(2, n+1):
num[i] = i
for i in range(2, int(math.sqrt(n))+1):
if num[i] != 0:
for j in range(i+i, n+1, i):
num[j] = 0
for i in range(m, n+1):
if num[i] != 0:
print(num[i])
(정답)
from sys import stdin
import math
m, n = map(int, stdin.readline().split())
num = [0] * (n+1)
for i in range(2, n+1):
num[i] = i
for i in range(2, int(math.sqrt(n))+1):
if num[i] != 0:
for j in range(i*i, n+1, i):
num[j] = 0
for i in range(m, n+1):
if num[i] != 0:
print(num[i])
반복의 시작을 i+i가 아닌 i*i로 하면 시간을 줄일 수 있다. 시간복잡도 측면에서 유의미한 차이는 없지만 시간이 약간 줄어든다. 데이터가 커질수록 더 효과 높아질 것 같다. 참고로 이렇게 해도 결과가 똑같은 이유는 i에 i보다 작은 수를 곱한 것에 대해서는 앞에서 전부 살폈기 때문이다. (i의 약수의 배수를 검사할 때) (정답)


시간은 약 40ms 정도 차이가 난다.
038. 거의 소수 구하기 (백준 1456번)

https://www.acmicpc.net/problem/1456
from sys import stdin
import math
m, n = map(int, stdin.readline().split())
num = [0] * (n+1)
cnt = 0
for i in range(2, n+1):
num[i] = i
for i in range(2, int(math.sqrt(n))+1):
if num[i] != 0:
for j in range(i+i, n+1, i):
num[j] = 0
for i in range(2, n+1):
if num[i] != 0:
tmp = num[i]
while num[i] <= n / tmp:
if num[i] >= m / tmp:
cnt += 1
tmp = tmp * num[i]
print(cnt)
처음에는 이렇게 n+1 까지 배열을 만들어 소수 판정을 했다. 그랬더니 메모리 초과... (오답)
from sys import stdin
import math
m, n = map(int, stdin.readline().split())
num = [0] * 10000001
cnt = 0
for i in range(2, 10000001):
num[i] = i
for i in range(2, int(math.sqrt(10000001))+1):
if num[i] != 0:
for j in range(i+i, 10000001, i):
num[j] = 0
for i in range(2, 10000001):
if num[i] != 0:
tmp = num[i]
while tmp * num[i] <= n:
if tmp * num[i] >= m:
cnt += 1
tmp = tmp * num[i]
print(cnt)
책을 보니 소수의 제곱수를 구하는 것이기 때문에 굳이 10^14까지 소수를 확인할 필요 없이 10^14의 제곱근인 10^7까지만 확인하면 된다고 한다. 그렇게 수정하고 제출했더니 해결되었다. (정답)
추가로, 책에서는 n제곱한 값을 구하는 도중 값이 변수 표현 범위를 초과하는 경우가 있어, 계산 오류를 방지하려면 num[i] <= n / tmp 이런식으로 넘겨서 계산하는 것이 좋다고 나와있다. 이 문제에서는 이렇게 하지 않아도 딱히 문제될 게 없었지만 나중에 혹시 계산 오류를 만나게 되면 떠올리면 도움이 될 만한 내용인 것 같다.
039. 소수&팰린드롬 (백준 1747번)

https://www.acmicpc.net/problem/1747
from sys import stdin
import math
MAX = 10000001
n = int(stdin.readline())
num = [0] * MAX
for i in range(2, MAX):
num[i] = i
for i in range(2, int(math.sqrt(MAX))+1):
if num[i] != 0:
for j in range(i+i, MAX, i):
num[j] = 0
for i in range(n, MAX):
if num[i] != 0:
isP = True
tmp = str(num[i])
for j in range(0, len(tmp)//2):
if tmp[j] != tmp[len(tmp)-j-1]:
isP = False
break
if isP:
print(num[i])
break
소수를 찾은 다음에 그게 팰린드롬인지만 확인하면 되는 간단한 문제. (정답)
040. 제곱 ㄴㄴ수 (백준 1016번)

https://www.acmicpc.net/problem/1016
from sys import stdin
import math
min, max = map(int, stdin.readline().split())
num = [True] * (max - min + 1)
cnt = 0
for i in range(2, int(math.sqrt(max)) + 1):
pow = i * i
tmp = (min + pow - 1) // pow * pow
while tmp <= max:
num[tmp-min] = False
tmp += pow
for i in range(0, max - min + 1):
if num[i]:
cnt += 1
print(cnt)
어우 문제 이해하는 데에도 한참 걸렸던 문제... 힘들게 풀었다... (정답)
from sys import stdin
import math
min, max = map(int, stdin.readline().split())
check = [True] * (max - min + 1)
cnt = 0
# 소수 구하기
rng = int(math.sqrt(max)) + 1
num = [0] * (rng)
for i in range(2, rng):
num[i] = 1
for i in range(2, int(math.sqrt(rng))+1):
if num[i] != 0:
for j in range(i+i, rng, i):
num[j] = 0
# 소수의 제곱수로 나누어 떨어지는지 체크
for i in range(2, rng):
if num[i] != 0:
pow = i * i
tmp = (min + pow - 1) // pow * pow
while tmp <= max:
check[tmp-min] = False
tmp += pow
for i in range(0, max - min + 1):
if check[i]:
cnt += 1
print(cnt)
추가로, 모든 수에 대해서 제곱을 하고 배수를 없애는 것보다 소수의 제곱에 대해서만 배수를 체크하는 것이 더 빠르다. 첫번째 풀이에 에라토스테네스의 체만 추가한 풀이다. (정답)


오 140ms 차이..!!
07-2. 오일러 피
041. GCD(n, k) = 1 (백준 11689번)
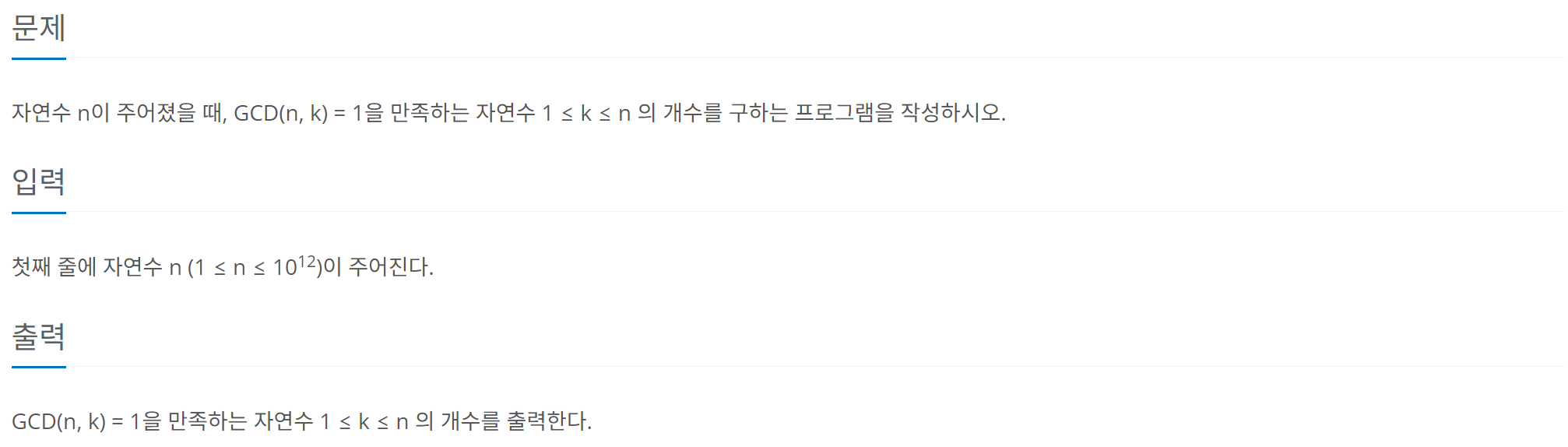
from sys import stdin
import math
n = int(stdin.readline())
ans = n
for i in range(2, int(math.sqrt(n)) + 1):
if n % i == 0:
ans = ans - ans // i
while n % i == 0:
n = n // i
if n > 1:
ans = ans - ans // n
print(ans)
이것도... 겨우 겨우 이해한 문제 ㅠㅠ (정답)
07-3. 유클리드 호제법
042. 최소공배수 (백준 1934번)
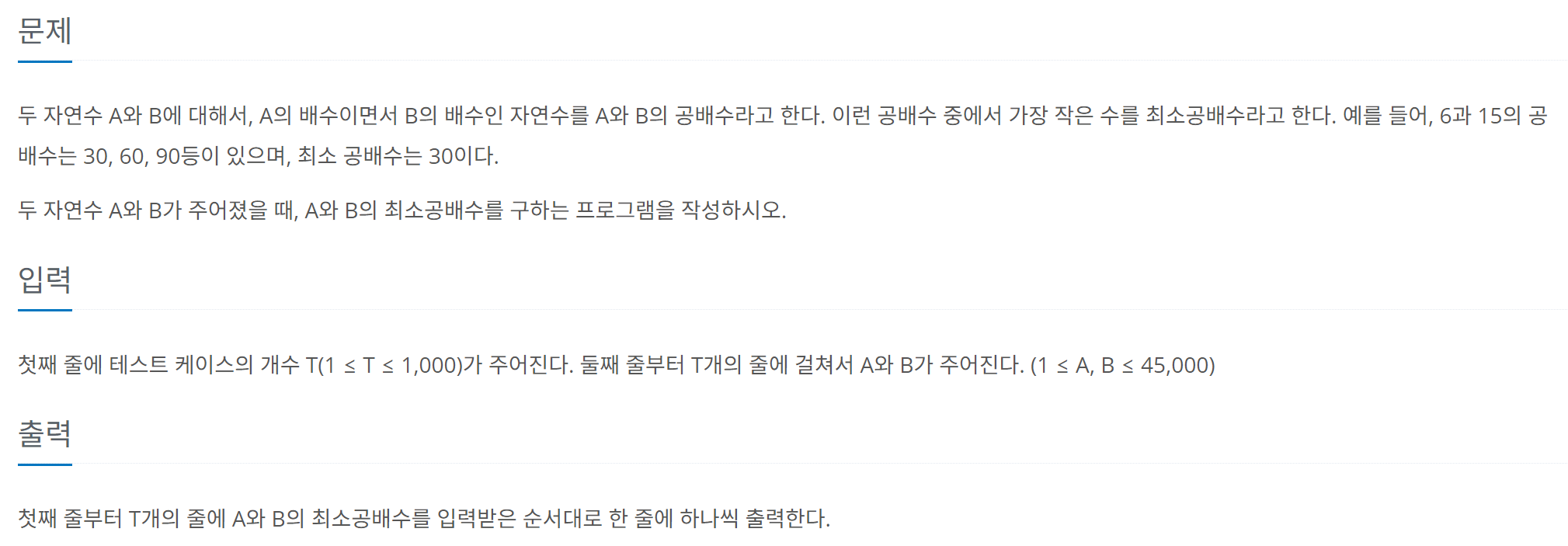
https://www.acmicpc.net/problem/1934
from sys import stdin
def gcd(a, b):
if b == 0:
return a
else:
return gcd(b, a % b)
n = int(stdin.readline())
for _ in range(n):
a, b = map(int, stdin.readline().split())
print(int(a * b / gcd(a, b)))
이산수학에서 배웠던 유클리드 호제법! (정답)
043. 최대공약수 (백준 1850번)

https://www.acmicpc.net/problem/1850
from sys import stdin
def gcd(a, b):
if b == 0:
return a
else:
return gcd(b, a % b)
a, b = map(int, stdin.readline().split())
cnt = gcd(a, b)
print("1" * cnt)
규칙을 찾아서 풀어야 했던 문제. 근데 원리는 잘 모르겠다... (정답)
'Group > EDOC' 카테고리의 다른 글
| EDOC 2023-W 1회차 정모 기록 (0) | 2024.01.09 |
|---|---|
| EDOC 2023-W 1회차 정모 (0) | 2024.01.09 |
| EDOC 2023-2 7주차 과제 (1) | 2023.11.27 |
| EDOC 2023-2 7회차 정모 (1) | 2023.11.27 |
| EDOC 2023-2 6주차 과제 (0) | 2023.11.27 |



